CRADLE CFD YAZILIMI BATARYA MODELLEME
PREPARED BY |
M. Ahmet Kozanoğlu Lider CFD Mühendisi |
Giriş
Batarya, kimyasal bir reaksiyon yoluyla elektrik (enerji) üreten veya şarj yoluyla elektrik enerjisini depolayan bir cihazdır. Cradle CFD içerisinde, batarya modeli termal/elektrik analizinde aşağıda yer alan verileri çıkartmak veya bu verilerle analiz eylemi gerçekleştirmek için uygulanır.
- Giriş/çıkış gücü (akım ve voltaj)
- Batarya ısı üretimi
Bataryanın temel amacı, güç girişi ve çıkışıyla birlikte depolanan enerjiyi saklayarak/koruyarak gerekli olduğunda kullanılmasını sağlamaktır; ancak ikincil ve kaçınılmaz olarak enerji kaybı nedeniyle ısı üretimi de meydana gelir. Bu olguları aynı anda gözlemlemek tasarımın iyileştirilmesi adına çok önemlidir; ancak yapılacak simülasyonun hedefi bataryanın termal yönetimine odaklandığında elektrik hesaplaması ihmal edilebilir. Cradle CFD içerisinde kullanıcılar isteğe bağlı olarak batarya modelini yalnızca ısı üretim kaynağı olarak kullanabilmektedir.
Cradle CFD içerisinde iki farklı batarya modeli kullanılabilir. Bunlar sırasıyla;
- Eşdeğer Devre Modeli (RC modeli)
Basit elektrik devre elemanlarını birleştirerek bataryanın davranışını ve cevaplarına istinaden model oluşturmaktadır. OCV'yi (Açık Devre Voltajı) varsayarak ve birden fazla elektrik direnci ve kapasitör kombinasyonunu bağlayarak, bataryanın elektriksel ve termal tepkisi modellenebilir.
Li (lityum) iyonlaşmasının kimyasal reaksiyonu, elektrolit içindeki lityum iyonlarının çözücüde dağılıp hareket etmesi ve -/+ elektrodun katısında bulunan lityumun hareket edip dağılmasının mikroskobik boyutunu kullanarak model oluşturmayı sağlar. Her birini tek boyutta simüle ederek bataryanın davranışını yeniden temsil eden bir modeldir. Birçok referansta olduğu gibi, mikroskobik tek boyutlu lityum difüzyon denklemi, lityum iyonlaşma kinetiği ve elektrik alanları birleştirilmiştir. Sonuç, bataryanın çıkış voltajı ve ısıyla dağıtılan enerjidir.
Eşdeğer Devre Modeli (RC modeli)
Bu modelin detayları için [1] numaralı referansta yer alan çalışmadan yararlanılabilir. Şekil 1'de gösterildiği gibi, batarya tepkisini yeniden üretmek için seri direnç "R_series" ve RC paralel ağları kullanılır. Açık devre voltajı "OCV(z(t))", şarj oranına "z(t)" bağlı bir değer olarak hesaplanır.
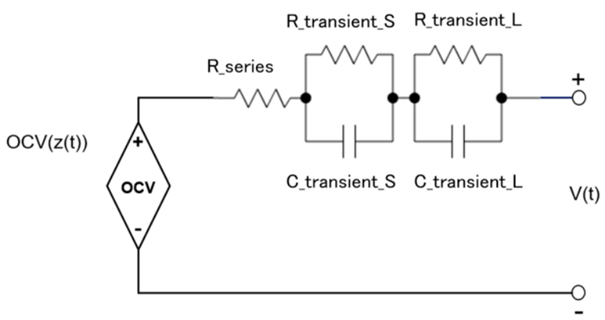
Şekil 1 Eşdeğer devre modelinin devre şeması
Açık devre voltajı (OCV)
Şekil 1'deki "OCV(z(t))" açık devre voltajını temsil eder. Bu, geçmiş kullanım durumuna ve akıma bağlı olmayan ideal bir voltaj kaynağı olarak kabul edilir. Pratikte, şarj veya deşarj olmaksızın sabit bir durumdaki bataryanın açık devre terminal voltajı olarak ölçülür ve esas olarak "z(t)" şarj durumuna bağlıdır (Ayrıca sıcaklığa da bağlıdır.).
Şarj durumu (SOC)
Bataryanın şarj oranını temsil eder. SOC, batarya kapasitesi [Ah] için şarj oranını temsil eder ve tam şarj %100'dür. 0 ile 1 arasında bir aralık olarak tanımlanır ve "z(t)" ile temsil edilir.
Seri direnç
Açık devre voltajıyla seri haldeki bir elektrik direnci olan seri direnç "RI" (R_series) anlık voltaj düşüşünü oluşturulur. Hem şarj hem de deşarj, eşdeğer devre modelinde enerji kaybının ana kaynağı olan voltaj düşüşüne neden olur.
RC paralel devre
Şekil 1, bir direnç elemanı (resistor-R) ve bir kapasitörün (C) RC paralel devrelerini içerir. Bu, batarya voltajının geçici tepkisini yeniden üreten bir elektrik devresi modelidir. Kısa süreli ve uzun süreli geçici tepkileri yeniden üretmek için atanmış iki set RC paralel devresi vardır. Kısa süreli tepki "RS" (R_transient_S) ve "CS" (C_transient_S) tarafından ve uzun süreli tepki "RL" (R_transient_L) ve "CS" (C_transient_L) tarafından oluşturulur.
Hesaplama prosedürü
Uygulanan eşdeğer devre modelinde, batarya karakteristiği aşağıdaki parametrelerle belirtilir.
Batarya kapasitesi Q [Ah]
Açık devre voltajı OCV [V]
Seri direnç RI [Ω]
RC paralel devresinin kapasitansı ve elektrik direnci CS, CL [C], RS, RL [Ω]
Bu değerler eşdeğer devre modeli kullanıldığında girilmesi gereken parametrelerdir, sabit sayı olarak girilebilir ve aynı zamanda "z" şarj durumunun bir fonksiyonu olarak verilebilir. Bu modelde parametreler “z” şarj durumunun üslerinin ve polinomlarının toplamları olarak ifade eder. Ayrıca bir komut dosyası veya kullanıcı işlevi kullanılarak sıcaklığa bağlı hale getirilebilir.
Prosedür;
- SOC değeri "z" hesaplanacaktır: Başlangıç değeri kullanıcı girişiyle verilir. Bataryadan geçen elektrik akımı yolundan her döngü için z'yi güncellenecektir.
- OCV, RS, CS, RL, CL, RI'yi hesaplanacaktır: Bu parametreler z'nin fonksiyonlarıdır. Komut dosyası sıcaklık bağımlılıklarını da hesaba katabilir.
- Bataryadan geçen akım yolundan gelen tepki voltajını hesaplanacaktır: Elektrik devresi hesaplamasıyla elde edilir. Aşağıdaki denklem çözülür.
- Batarya tarafından yayılan enerjiden üretilen ısı miktarını hesaplanacaktır.

P2D modeli
Bu model, bataryanın enerji dengesinden sorumlu iyonlaşma kimyasal reaksiyonu ile çalışır. Li (lityum) bataryaları esas olarak varsayılır ve iyonlaşma reaksiyon hızı Butler-Volmer denklemi ile verilir. Ek olarak, lityumun konsantrasyon dağılımı ve difüzyonu buna göre ele alınır. Lityum sadece elektrolitte değil, aynı zamanda her iki elektrotun katı parçacıklarında da depolama görevi gördüğünden, katı parçacıklardaki difüzyon ve elektrolit içindeki difüzyon birlikte ele alınır. Ayrıca, akım elektrolit ve her iki elektrottan geçtiğinden, elektrik alanı ve akım dağılımını aynı anda çözmek gerekir. Bu, tüm bu sorunları çözen ve temel fiziksel denklemlere dayanarak bataryanın içindeki mikro ölçekli Li konsantrasyon dağılımını ve elektrik alanını hesaplayan bir yöntemdir (Referans [2] ).
Bataryanın iç mikro yapısı
Bataryanın P2D modelinin varsayımı olarak, aşağıda yer alan iç mikro yapısı baz alınabilir: (Referans [3] [4]). Bataryalar aslında bu şekilde bir yapıda üretilir detaylı bilgi için bataryanın mikroskobik fotoğraflarını içeren referanslar incelenebilir. [3], [5]
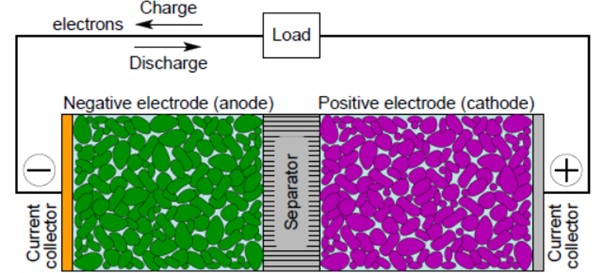
Şekil 2 Batarya iç mikro yapısı
- Akım toplayıcılar, her iki elektrodun uçlarında paralel ve birbirine bakacak şekilde düzenlenmiştir. Akım toplayıcı için alüminyum gibi bir iletken kullanılır.
- Her elektrodun katı malzemesi, akım toplayıcıların içinde gözenekli bir durumda düzenlenmiştir. Bu katı malzemeler hem elektriksel iletkendir hem de lityum depolanmasıdır.
- Elektrodun katı malzemesi, lityum içeride depolanabilmesi için delikli bir moleküler yapıya sahiptir ve lityum yalnızca katı yüzeye değil, aynı zamanda içeriye de nüfuz eder. Ayrıca, lityum iyonlaşma reaksiyonunu destekleyen gözenekli yapı nedeniyle yüzey alanı büyüktür.
- Negatif elektrotta katı malzeme olarak genellikle grafit kullanılır ve lityum yüksek enerji durumunda tutar. Tersine, pozitif elektrottaki katı malzemeler çeşitli olmasına rağmen, lityum düşük enerji durumunda tutulur ve enerji boşluğu bataryanın elektromotor kuvvetini oluşturur. Lityumun negatif elektrottaki katı malzemede depolandığı durum yüklü durumdur ve lityumun pozitif elektrottaki katı malzemede depolandığı durum deşarj durumudur. İki katı malzeme arasında yalıtım için bir ayırıcı vardır. Ayrıca gözeneklidir.
- Negatif elektrot, ayırıcı ve pozitif elektrot katıları gözenekli gövdelerdir ve aralarındaki boşluklar lityum iyonları içeren elektrolit ile doldurulur. Elektrotlar arasında lityum taşımak için vazgeçilmez bir ortamdır.
Bataryaların mikro yapısının modellenmesi
Yukarıda yer alan Şekil 2'deki batarya iç mikro yapısı P2D modeli için batarya iç yapısının şematik diyagramı bataryanın iç mikro yapısı, lityumun mikro yapı içindeki difüzyon hareketi ve elektrik alanı/akımı simüle edilebilecek şekilde basitçe modellenmiştir. Şekil 3 bunu şematik olarak göstermektedir.
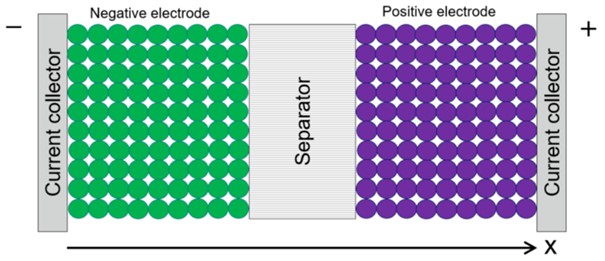
Şekil 3 P2D modeli için batarya iç yapısının şematik diyagramı
- Elektrodun gözenekli gövdesinin katı malzemesi, "birçok küresel parçacıktan" oluşan bir paketleme kutusu olarak modellenmiştir. Ayrıca, bu parçacıkların çaplarının tekdüze olduğu varsayılmaktadır.
- Negatif elektrot katı malzemesi, ayırıcı ve pozitif elektrot katı malzemesi, Şekil 3'te gösterildiği gibi tekdüze bir şekilde düzenlenmiştir ve lityum konsantrasyonunun, elektrik alanının ve akımın tek boyutlu olarak hesaplanabileceği varsayılmıştır.
- Negatif kutup toplayıcısından pozitif kutup toplayıcısına kadar olan uzaysal tek boyutlu ekseni x ekseni olarak alınabilir.
Son maddede yer alan durum neticesinde, x ekseni yönünde tek boyutlu bir simülasyonun yapılması mümkündür. Ayrıca, bireysel küresel parçacıkları radyal yönde bölerek, lityum elektrotun katı malzemesine nüfuz etme süreci de Şekil 4'te gösterildiği gibi gerçekleştirilebilir. Radyal r eksenini x ekseninden bağımsız alarak, lityum konsantrasyon dağılımı elektrotun katı malzemesinin içinde iki boyutta (x,r) hesaplanır.
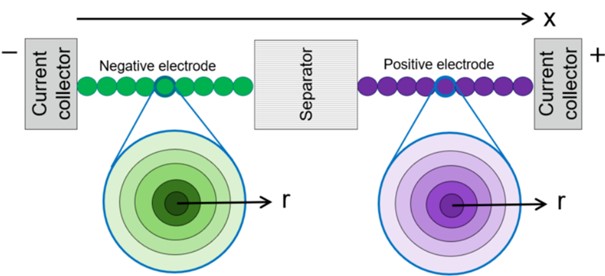
Şekil 4 Mikro yapıdaki bireysel parçacıkların şematik diyagramı
- Lityumun iyonlaşma reaksiyonu küresel parçacıkların en dış kabuğunda meydana gelir. İyonize Li iyonları parçacıkların dışındaki elektrolit içinde yayılır ve hareket eder.
Yukarıda belirtilen durum bataryanın içindeki mikro yapının modellemesidir. Bu modelleme, lityumun düşük boyutlardaki difüzyon ve konsantrasyon dağılımını simüle etmeyi mümkün kılar. Elektrik alanının ve lityum iyonizasyon reaksiyon hızının temel fiziksel denklemleriyle birleştirerek çözmeyi kolaylaştırır.
Çözülmesi gereken temel denklemler aşağıdaki gibi sıralanmıştır. Bu denklemler simülasyon esnasında farklı zamanlarda kullanılarak çözüme katkıda bulunmaktadır.
- Katı malzemelerde yük korunumu
- Elektrolitte yük koruma denklemi
- Butler-Volmer denklemi
- Lityum difüzyon denklemi (kütle korunumu): elektrotun katı parçacıklarında
- Lityum difüzyon denklemi (kütle korunumu): elektrolitte
Yapılan analizlerde aşağıdaki maddeler kabul edilerek simülasyon gerçekleştirilir.
- Batarya, bir durum değişkeni olarak şarj durumunu korur. Şarj ve deşarj nedeniyle zamanla değişen parametreler içerdiğinden, geçici hesaplamalarda kullanılır.
- Batarya modeli ısı hesaplamasıyla kullanılmalıdır, ancak akım hesaplaması gerekli değildir.
- Batarya modeli, bataryanın iç direncinden kaynaklanan batarya ısısı üretimini ele alır. Ayrıca, akım hesaplamasından kaynaklanan Joule ısınması akım hesaplamasında ele alınır, bu nedenle batarya modelinde ele alınmaz.
Kaynakça
[1] | M. Chen and G. A. Rincon-Mora, "An accurate electrical battery model capable of predicting runtime and I–V performance", IEEE Trans. Energy Convers., vol. 21, no. 2, pp. 504-511, Jun. 2006. |
[2] | "Simulation and Optimization of the Dual Lithium Ion Insertion Cell", Thomas F. Fuller,* Marc Doyle,* and John Newman J. Electrochem. Soc., Vol. 141, No. 1, January 1994. |
[3] | Gregory L. Plett and Kanhao Xue, "MODELING, SIMULATION, AND IDENTIFICATION OFBATTERYDYNAMICS", Chapter 3 "Microscale Cell Models", Lecture notes, Colorado Univ. ECE5710, 2018. |
[4] | Ali Jokar, Barzin Rajabloo, Martin Desilets, Marcel Lacroix, "Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries", Journal of Power Sources, 2016. |
[5] | Chang-Hui Chen et al. "Development of Experimental Techniques for Parameterization of Multi-scale Lithium-ion Battery Models", Journal of The Electrochemical Society, 2020 167 080534 |







