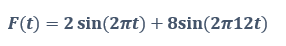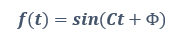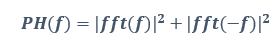ADAMS POSTPROCESSOR – FAST FOURIER TRANSFORM (FFT)
Hazırlayan: Deniz ASLAN (Mekanik Simülasyon Aday Mühendisi)
Evrendeki birçok olay (ses, elektromanyetik dalgalar, titreşim, sinyal vb.) bir dalga fonksiyonu olarak tanımlanabilir. Evrende gözlemlenen bütün dalga formları aslında farklı genlik ve frekans değerlerine sahip sinüs fonksiyonlarının toplamından ibarettir. Sinüs fonksiyonları dalgaların asıl karakteristiğini oluşturan unsurlardır. Zaman tabanındaki (time domain) dalga fonksiyonları genellikle karmaşık yapıdadır ve zamana bağlı değişimi gösterirler. Bu sebeple bir dalgayı zaman tabanında incelemek daha zorlu bir iştir ve yanlış yönlendirici olabilir. Dalga yapılarını daha iyi anlamak ve temel özelliklerini ortaya koyarak bir dalga fonksiyonunu detaylıca incelemek için dalga fonksiyonları zaman tabanından frekans tabanına (frequency domain) çevrilebilmektedir.
Bu yazıda zaman tabanından frekans tabanına dönüşümü sağlayan FFT (Fast Fourier Transform) ve FFT’nin Adams’ta kullanımı anlatılmıştır.
FFT; dalga fonksiyonlarını, birleştirildiklerinde kendisini oluşturan sinüs dalga formlarına dönüştüren matematiksel bir dönüşüm fonksiyonudur. Temel olarak fonksiyonun frekans spektrumunu elde etmek için kullanılarak, fonksiyonun içerdiği farklı frekanslardaki bileşenlerin belirlenmesini mümkün kılmaktadır. Bu yöntem ile dalga yapı taşlarına ayrılarak, dalga fonksiyonunun her açıdan detaylı şekilde incelenip kendisini oluşturan bileşenlerin ayırt edilebilmesini sağlamaktadır.
FFT, özellikle büyük veri setleri üzerinde hızlı ve etkili bir şekilde çalışabilen bir algoritma olduğundan, gerçek zamanlı uygulamalar ve büyük veri analizi gibi birçok alanda yaygın olarak kullanılmaktadır. FFT'nin hızı ve verimliliği, bilgisayarlar ve dijital işleme teknolojilerindeki ilerlemelerle birleşerek titreşim analizleri, sinyal işleme, ses işleme, görüntü işleme ve birçok başka alanda önemli bir araç haline gelmesini sağlamıştır.
1. ADAMS İLE FFT UYGULAMASI
Adams içerisinde oluşturulan modelden bir simülasyon gerçekleştirildikten sonra PostProcessor ekranında istenilen bir ölçümün grafiği çizdirilebilmektedir. Elde edilen grafiği zaman tabanından frekans tabanına dönüştürmek için sırasıyla “Plot → FFT” seçenekleri takip edilebilir.
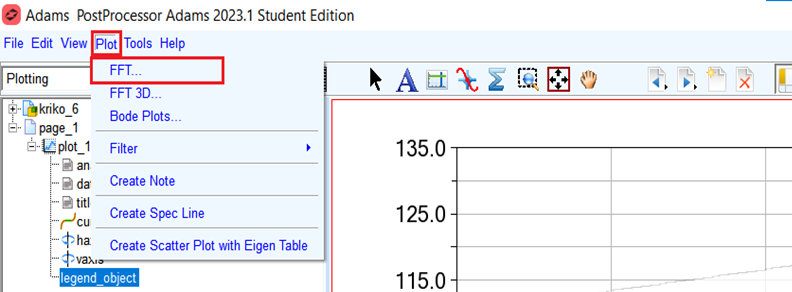
Şekil 1 – PostProcessor Arayüzünde FFT Butonu
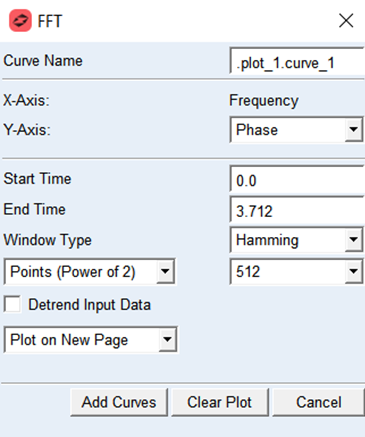
Şekil 2 – FFT Oluşturma Penceresi
FFT oluşturma penceresindeki ifadeler aşağıda açıklanmıştır:
- Curve Name: Bu seçenek ile dönüşüm uygulanacak eğri veya eğriler seçilmektedir.
- Y Axis: Y ekseni için “Mag, Phase, PSD” seçeneklerinden uygun olanı tercih edilmektedir.
- Dönüştürülmek istenen zaman aralığına göre başlangıç ve bitiş zamanı değerleri girilmektedir.
- Window Type: Dönüşüm sırasında kullanılması istenen pencereleme metodu seçilmektedir.
- Points (Power of …): Dönüşümde kaç interpolasyon noktası olacağı seçilmektedir. (2’nin çift kuvvetlerinin seçilmesi tavsiye edilmektedir.)
- Detrend Input Data: Giriş verilerini azaltma seçeneği ile, verilerdeki zaman içindeki kaymalar ortadan kaldırılmaktadır. Postprocessor tarafından verilere doğrusal bir regresyon uygulanmaktadır ve dönüşüm gerçekleşmeden önce bu kaymalar verilerden çıkartılmaktadır.
- Add Curves: FFT eğrisini çizdirmek için kullanılmaktadır.
- Clear Plot: FFT eğrisini silmek için kullanılmaktadır.
1.1 FFT Uygulama Ayarları
1.1.1 Y – Axis
Adams PostProcessor, verileri frekans tabanında sunmak için üç farklı metoda sahiptir:
 Şekil 3 – Y Ekseni Seçenekleri
Şekil 3 – Y Ekseni Seçenekleri
- FFTMAG: FFT algoritmasından gelen karmaşık sonucun büyüklüğünü hesaplamaktadır. Adams PostProcessor tarafından frekans verisinin sadece sol tarafı çizdirilmekte ve grafiğin sağ tarafı, sol tarafın bir ayna görüntüsü olarak kullanılmaktadır.
Adams PostProcessor, FFTMAG verilerini zaman tabanı örneklerinin sayısı olan N'nin yarısı (N/2) ile ölçeklendirmektedir. Bu, FFTMAG zirvesinin zaman tabanı verilerinin büyüklüğünde temsil edilmesini sağlamaktadır. 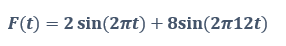
FFTMAG grafiğinde, 1 Hz'de iki tepe noktası ve 12 Hz'de sekiz tepe noktası bulunmaktadır.
FFTMAG özellikle sistemlerin doğal frekanslarını hesaplama konusunda çok kullanışlı olabilmektedir.
- FFTPHASE: FFTPHASE, standart FFT algoritmasından dönen karmaşık değerin faz açısını belirler. Belirli bir frekansta FFTPHASE, zaman taban verilerinde temsil edilen eşdeğer sinüs fonksiyonunun faz kaymasını gösterir. Bir sinüs fonksiyonunun faz kayması aşağıdaki formüldeki “Φ” değeridir.
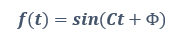
- PSD (Power Spectral Density): Zamana bağlı herhangi bir sinyal, zaman ve frekans tabanlarında aynı büyüklüğe sahiptir. Spektral analizde önemli olan bir frekans aralığı boyunca sahip olunan güç miktarıdır. PSD grafiği, sinyalin kendi frekans bileşenleri arasındaki güç dağılımını ifade etmektedir. FETMAG grafiğine benzer bir görünüme sahiptir ancak grafik, farklı ölçekte çizilmektedir. PSD metodunda kullanılan ölçekleme formülü aşağıdaki gibidir:
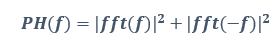
PSD metodunda, Pwelch fonksiyonu kullanılmaktadır. PSD toplamı, orijinal sinyal büyüklüğünün karesinin zamana göre integraline eşittir. Pwelch fonksiyonu, PSD hesaplarken Welch metodununu kullanmaktadır.
1.1.2 Window Type (Pencereleme Çeşitleri)
FFT algoritması, zaman tabanındaki veriyi sonlu ve sürekli olan bir veri serisinin periyodik bir aralığı olarak değerlendirmektedir. Bu sebeple başlangıç ve bitiş değerleri de aynı kabul edilerek seçilen aralıktaki süreksizlerin giderilmesi ve başlangıç – bitiş değerlerinin aynı olması sağlanmaktadır. Adams içindeki pencereleme fonksiyonları bu süreksizlikleri giderip incelenen aralığın periyodik olmasını sağlayan araçlardır. Adams içerisinde birden fazla pencereleme fonksiyonu bulunmakta ve bu fonksiyonların her biri farklı formüller kullanarak işlem gerçekleştirmektedir.
Birim adım girdi fonksiyonlarına benzeyen pencereleme fonksiyonları, FFT fonksiyonlarının çıkış genliklerini korurken, FFT bütünlüğü kaybolmadan önceki minimal süreksizlikleri kabul etmektedir. Benzer bir şekilde tepe frekans genliklerinin doğrulunu azaltma eğiliminde olan pencereleme fonksiyonları, bitiş noktasındaki süreksizliklerin getirdiği negatif etkileri büyük ölçüde azaltmaktadır.i
Aşağıda pencereleme fonksiyonlarının formülleri belirtilmiştir:

Şekil 4 – Pencereleme Fonksiyonları [i]
Denklemlerdeki Wj sembolü fonksiyonu, N ise girdi örneklem sayısını ifade etmektedir.
Genel olarak, dikdörtgen pencereleme fonksiyonu, ideal genlikleri en doğru şekilde ifade eder, ancak süreksizliklere en duyarlı olan fonksiyondur. Hanning pencereleme fonksiyonu, en büyük süreksizlikleri filtreler ancak ideal genlikleri en az doğrulukla temsil eder. Hangi fonksiyonun kullanılacağı yapılan işe ve kullanıcının tercihine göre değişmektedir.
- Dikdörtgen Pencereleme Fonksiyonu: Dikdörtgen pencereleme, toplanan veri periyodik ise hiçbir frekans veya genlik bozulması oluşturmamaktadır. Eğer sinyal periyodik değilse oluşan genlik hatası maksimum olmakta ve frekans içeriği bütün bant genişliğine yayılmaktadır. Dikdörtgen pencereleme;
- Ölçüm süresinde tamamen sıfırlanan darbe ölçümlerinde
- Ölçüm süresi ile tamsayı ilişkisi olan sinüzoidal sinyallerde
kullanılabilmektedir.
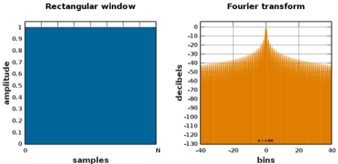
Şekil 5 – Dikdörtgen Pencereleme Fonksiyonu [ii]
- Hanning Pencereleme Fonksiyonu: Hanning pencereleme fonksiyonu operasyonel gürültü ve titreşim analizleri yaparken sık kullanılan bir fonksiyondur. Başlangıç ve bitiş noktalarındaki kesintilerden dolayı oluşan spektral sızıntıları (spectral leakage) gidermek için de Hanning Fonksiyonu en yaygın kullanılan seçeneklerden biri olmaktadır. Hanning fonksiyonu, diğer pencereleme fonskiyonlarına göre, alınan frekans spekturumunun genlik ve frekans çözünürlüğü üzerinde ortalama bir etkiye sahip olduğundan genellikle rastgele verilerle kullanılmaktadır.
Hanning pencerelemesi;
- Hareket halindeki bir aracın çıkardığı ses dalgasında
- Bir pompanın çalışırken yaydığı titreşim dalgasında
Kullanılabilmektedir.
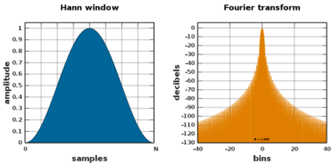
Şekil 6 – Hanning Pencereleme Fonksiyonu [ii]
- Hamming Pencereleme Fonksiyonu: Hamming pencereleme fonksiyonu, sinyalin başlangıç ve bitiş kısımlarında düşük geçişli bir pencereleme sağlamaktadır. Bu, sinyalin sürekli olmayan yapısından kaynaklanan spektral sızıntıyı azaltmaya yardımcı olarak frekans bileşenlerinin daha doğru bir şekilde belirlenmesini sağlamaktadır.
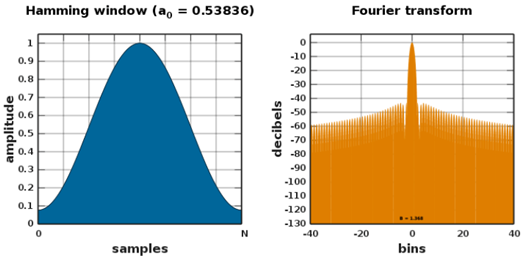
Şekil 7 – Hamming Pencereleme Fonksiyonu [ii]
- Welch Pencereleme Fonksiyonu: Welch pencereleme fonksiyonu, sinyalin örnekleme aralığını parçalara bölerek her bir parçaya ayrı ayrı FFT uygulamakta ve bu parçaların güç spektrumlarını birleştirmektedir.
Welch fonksiyonu, özellikle genlik spektrumlarının tahmin edilmesi gereken durumlarda ve veri pencerelenirken gürültünün etkilerini azaltmak için tercih edilebilmektedir. Örneğin, bir sinyaldeki belirli frekans bileşenlerinin güç spektrumlarının tahmin edilmesi gereken frekans analizi uygulamalarında Welch fonksiyonu sıklıkla tercih edilmektedir.
- Parzen Pencereleme Fonksiyonu: Parzen pencereleme fonksiyonu, parametrik olmayan yoğunluk tahmini için kullanılan bir pencereleme fonksiyonudur.
Parzen pencereleme fonksiyonunda, veri setinin bazı noktalarında belli genişliklerde pencereler oluşturularak her pencerenin merkezindeki veri noktalarının etkilerini baz alan yoğunluklar tahmin edilmektedir. Parzen pencereleme yöntemi, genellikle dağılım karakteristiği bilinmeyen veri setlerinde yoğunluk tahmini yapmak için kullanılmaktadır.
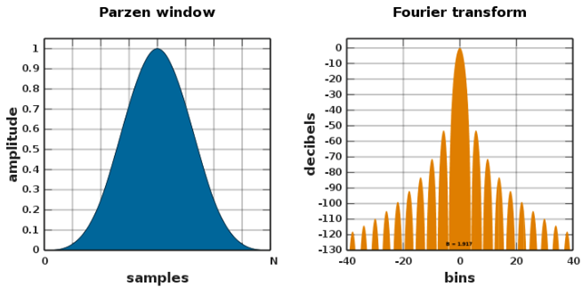
Şekil 8 – Parzen Pencereleme Fonksiyonu [ii]
- Bartlett Pencereleme Fonksiyonu: Bartlett pencereleme fonksiyonu kenarlarda sıfır olup pencere merkezinde maksimum genliğe sahip olan bir fonksiyondur. Merkezden kenarlara lineer değişen üçgen şekle sahiptir. Bartlett fonksiyonu, ana lobun daha geniş olduğu durumlarda tercih edilebilmektedir. Şeklinden dolayı Bartlett fonksiyonu yan loplarda daha yüksek genlikli sonuçlara sebep olarak spektral sızıntı ve frekans çözünürlüğünü olumsuz etkileyebilmektedir.
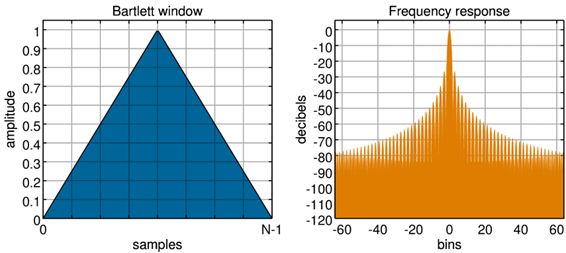
Şekil 9 – Bartlett Pencereleme Fonksiyonu [ii]
- Blackman Pencereleme Fonksiyonu: Blackman pencereleme fonksiyonunda ana lop ve iki yan lop olmak üzere üç ana unsur vardır. Bu fonksiyon ana lob ile yan loblar arasında daha yumuşak bir geçiş yaparak spektral sızıntıyı azaltmaktadır. Dikdörtgen ve Bartlett gibi fonksiyonlardan daha iyi bir spektral sızıntı önleme özelliğinden dolayı yaygın olarak kullanılabilmektedir.
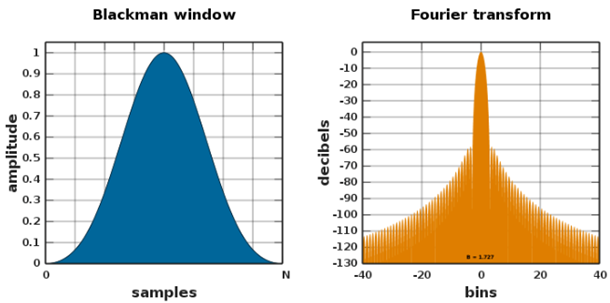
Şekil 10 – Blackman Pencereleme Fonksiyonu [ii]
- Triangular Pencereleme Fonksiyonu: Triangular pencereleme fonksiyonu, Bartlett fonksiyonuna benzemekte olup pencere uzunluğunun farklı olmasından dolayı ayrılmaktadır. Yan lobları diğer fonksiyonlara göre daha yüksek olduğundan sprektral sızıntılar daha fazla meydana gelmekte ve basit durumlar ya da bazı özel uygulamalarda kullanılsa da yüksek doğruluk gerektiren çalışmalarda diğer pencereleme fonksiyonları tercih edilebilmektedir.
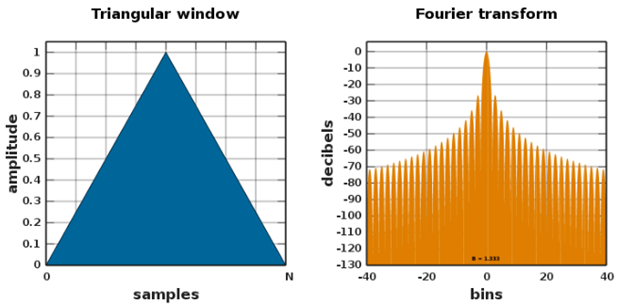
Şekil 11 – Triangular Pencere Fonksiyonu [ii]
1.1.3 Points (Power of …)
Nokta sayısı ile interpolasyon yapılan nokta adedi tanımlanmaktadır. Nokta sayısı ne kadar fazla olursa elde edilen sonuç o kadar gerçeğe yakın olabilmektedir. FFT uygulanırken, daha hassas ve doğru sonuçlar sunduğu için nokta sayısı “2”nin çift kuvvetlerinin kullanılması tavsiye edilmektedir.i

Şekil 12 – Nokta Seçimi
1.2 Adams FFT Grafik Örneği
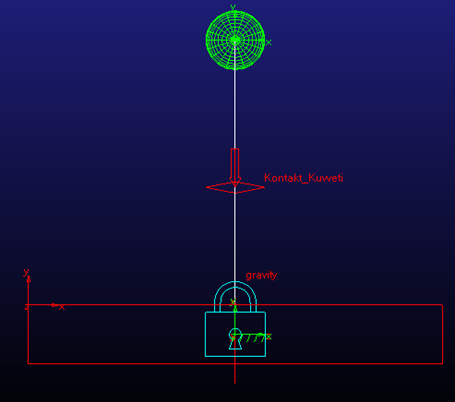
Şekil 13 – Serbest Düşüş Modeli
Şekil 13’te çelik bir zemin üzerine çelik bir topun serbest düşmesi modellenmiştir. Topla zemin arasındaki kontak kuvvetinin grafiği zaman tabanında çizdirildikten sonra FFT uygulanarak frekans tabanına dönüştürülmüştür. Şekil 14’te FFT grafiği gösterilmiştir.
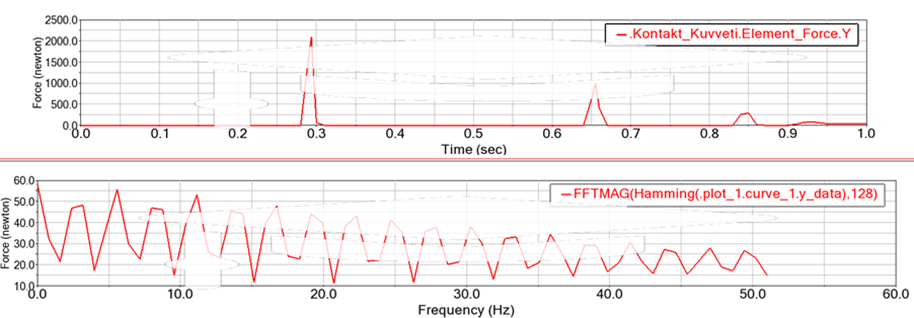
Şekil 14 – FFT Grafiği
Şekil 14’te Kuvvet-zaman grafiğinde görüldüğü üzere, top ve zemin arasındaki kuvvet her temasta bir tepe yapıp sonrasında sönümlenmiştir. Bu grafik FFT uygulanarak frekans tabanına dönüştürüldüğünde kuvvetin frekans aralığının 0 – 51Hz arasında olduğu ve hangi frekans değerlerinde kuvvetin tepe değerlere ulaştığı gözlemlenmiştir.
FFT uygulanırken FFTMAG metodu ve Hamming pencereleme fonksiyonu kullanılmıştır. Nokta sayısı 2128 olarak belirlenmiştir.
2. REFERANSLAR
- Adams 2023.1 Help Documentation
- Window Function, Wikipedia, https://en.wikipedia.org/wiki/Window_function